Get most out of factors of 224
Welcome factors of 224 to our blog post where we dive into the fascinating world of numbers and explore how they can be used to simplify math problems and enhance our daily lives. Today, we’re putting the spotlight on the number 224 and its factors. Numbers are not just a jumble of digits; they hold secrets and patterns that can unlock hidden doors in mathematics. By understanding the factors of 224, you’ll gain a powerful tool to unravel complex equations effortlessly. So grab your calculators, sharpen your pencils, and let’s uncover the magic behind this intriguing number!
What are Factors?
Factors, huh? You might be wondering what on earth they are and why they even matter. Well, fret not! Factors are simply the numbers that can be multiplied together to give a specific number. In other words, they’re like the building blocks of a number – the pieces that make it whole.
Let’s take the example of 224. Its factors would be all the different numbers we can multiply together to get 224 as a result. So, what could those factors possibly be? We’ll find out soon enough!
Understanding factors is crucial because they help us simplify complex math problems in various ways. By knowing the factors of a given number, we can break it down into smaller parts and work with them individually. This simplification allows us to tackle calculations more efficiently and accurately.
But wait, there’s more! Factors aren’t just confined to mathematics alone; they have practical applications in our daily lives too. From calculating measurements for recipes to determining optimal configurations for computer systems, knowing how to use factors can prove incredibly useful in real-world scenarios.
So now that we’ve established what factors are and why they matter beyond the realm of equations, let’s dive deeper into finding out exactly what makes up those elusive factors of 224!
Understanding the Number 224
Understanding the Number 224
When it comes to numbers, each one has its own unique characteristics and properties. One such number is 224. To truly understand this number, we must delve into its factors and explore how they can be used in various aspects of our daily lives.
So, what exactly are factors? In simple terms, factors are the numbers that can be multiplied together to give a particular number. For instance, the factors of 224 would be all the numbers that divide evenly into it without leaving a remainder.
Now let’s focus on the number itself – 224. This three-digit number may not seem significant at first glance, but when we start exploring its factors, we uncover hidden patterns and possibilities.
Finding the factors of 224 requires us to break down this number by dividing it by smaller integers starting from 1 and working our way up. By doing so, we discover that some of the factors include: 1, 2, 4, 7, and so on.
But why should we care about these factorizations? Well, knowing the factors of a number like 224 can actually come in handy in several real-life situations.
For example:
– When dealing with fractions or ratios involving quantities related to multiples of 224.
– Simplifying complex mathematical equations or expressions by factoring out common terms.
– Understanding relationships between different quantities within scientific experiments or data analysis where multiples or divisions by certain numbers might be involved.
– Identifying possible divisors or multipliers for problems related to dimensions or measurements.
By understanding how to use the factors of a given number like 224 effectively in these practical scenarios mentioned above (and many more), you’ll have an edge in simplifying your math problems and making connections across various disciplines.
However useful these factorizations may be in everyday life applications though; there are also challenges associated with working with them. Common mistakes when handling factors include miscalculations, overlooking certain factors, or misinterpreting their significance.
So, next
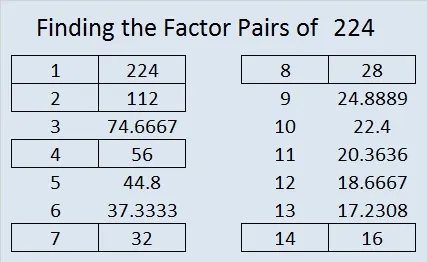
Finding the Factors of 224
When it comes to finding the factors of a number, like 224, it may seem daunting at first. But fear not! With a little bit of math know-how and some patience, you’ll be able to find those factors in no time.
To begin, let’s break down what factors are. Factors are the numbers that can be multiplied together to get a given number. In the case of 224, we want to find all the numbers that divide evenly into it.
So how do we go about finding these factors? One approach is to start with the smallest possible factor, which is 1. We then move on to dividing 224 by progressively larger numbers until we reach its square root or find all possible factors.
In this case, when we divide 224 by 2 (the next prime number), we get an even quotient of 112. Continuing our division process with other subsequent primes such as 2^4 =16 and so forth will lead us closer and closer towards getting all possible integer solutions for this particular problem.
By using this methodical approach and keeping track of each step along the way, you’ll soon have your list of factors for any given number!
Remember: practice makes perfect when it comes to finding factors efficiently. So keep at it and before you know it, factoring will become second nature!
How to Use Factors of 224 in Real Life
When it comes to using the factors of 224 in real life, you might be surprised at how often they can come in handy. Whether you’re working on a DIY project or trying to solve a math problem, understanding the factors of 224 can make your life a whole lot easier.
Let’s say you’re planning on building a bookshelf and want to ensure that its dimensions are just right. By knowing the factors of 224 (1, 2, 4, 7, 8, 14, 16, 28, 32…), you can easily determine which combinations will result in an even height or width. This saves you time and effort as you won’t have to guess or measure multiple times.
Similarly, if you’re faced with a math equation that involves multiples of 224, knowing its factors can help simplify the problem. You may be able to divide both sides by one of these factors and eliminate unnecessary calculations. This technique is particularly useful when dealing with larger numbers where mental math becomes more challenging.
The practical applications don’t stop there! Understanding the factors of any number allows us to work smarter rather than harder. It helps us break down complex problems into simpler ones and find efficient solutions. So whether it’s for measurements or mathematical equations – having knowledge about the factors of numbers like our friend here (224) is definitely beneficial!
With all these benefits in mind – from DIY projects to solving math problems – it’s clear that being familiar with the factors of numbers like our example here (224) has real-world applications that go beyond just number theory!
Tips for Using Factors to Simplify Math Problems
When it comes to solving math problems, factors can be your secret weapon. They provide a simple and effective way to break down numbers and make calculations easier. Here are some tips for using factors to simplify math problems.
When faced with a large number like 224, it’s helpful to find its prime factors. Prime factors are the building blocks of a number – they cannot be divided any further. By breaking down 224 into its prime factors (2 x 2 x 2 x 2 x 7), we can see that it is composed of smaller, manageable parts.
Next, look for common factors between numbers in a problem. For example, if you need to find the greatest common factor between two numbers, identify their prime factorization and look for shared primes. This will save you time by focusing on the essential elements.
Another tip is to use factors when simplifying fractions or ratios. By dividing both the numerator and denominator by their common factor(s), you can reduce them to their simplest form efficiently.
Factors also come in handy when working with algebraic expressions. They help with factoring polynomials or finding solutions for equations by identifying common terms or coefficients.
Remember that practice makes perfect! The more comfortable you become with using factors, the faster and more accurate your math problem-solving skills will become.
Incorporating these tips into your mathematical toolkit will undoubtedly enhance your problem-solving abilities and save you valuable time during exams or everyday calculations. So embrace the power of factors in simplifying math problems – they’re an invaluable tool!
Challenges and Common Mistakes when Working with Factors
Working with factors can be a helpful tool in simplifying math problems, but it’s not always smooth sailing. There are challenges and common mistakes that can trip you up along the way. Let’s explore some of these hurdles and how to overcome them.
One common mistake when working with factors is forgetting to consider all possible factors of a number. For example, when finding the factors of 224, it’s important to remember that negative numbers can also be factors. So, in addition to 1 and 224, -1 and -224 are also factors.
Another challenge is dealing with large numbers or prime numbers. Finding all the prime factors of a number like 224 may require more time and effort than finding the same for smaller or composite numbers. It becomes essential to have strong knowledge of multiplication tables or use tools like factorization methods.
Sometimes we mistakenly overlook common multiples between two different sets of factors while solving complex problems involving multiple variables or equations containing several unknowns such as algebraic expressions where factoring plays an integral role.
In addition, there may be instances where we incorrectly assume that a factor must be an integer. While this is often true, certain mathematical concepts deal with non-integer values as well (such as rational or irrational numbers), making it crucial to keep an open mind and consider all possibilities.
One challenge many people face is simply getting overwhelmed by long calculations involving multiple steps with various operations such as adding/subtracting fractions containing variable coefficients which lead us into incorrect answers due to careless errors from overlooking factoring techniques during intermediate steps causing misinterpretation in results generating inconsistencies within solutions resulting in inaccurate conclusions leading towards wrong final outcomes
Understanding the challenges associated with working with factors can help improve your problem-solving skills and avoid common pitfalls along the way
Conclusion: Why Knowing the Factors of 224 Can Be Useful in Daily Life
Knowing the factors of a number like 224 may seem like a trivial mathematical exercise, but it can actually have practical applications in daily life. By understanding and utilizing the factors of 224, you can simplify math problems, make calculations easier, and even find creative solutions to real-life situations.
Having an understanding of what factors are is essential. Factors are the numbers that can be multiplied together to get a given number. For example, the factors of 12 are 1, 2, 3, 4, 6 and 12 because these numbers can be multiplied together in various combinations to equal 12 (e.g., 3 x 4 =12 or even just multiplying by itself: e.g.,1×24=24).
Now let’s delve into the specifics of the number we’re focusing on – namely, why do we care about the factors of “224”? Understanding this number allows us to break it down into smaller components that provide valuable insights when solving mathematical equations or analyzing patterns.
Finding all possible factors for this specific case means listing out every whole number that evenly divides into it without leaving any remainder. In other words:
Factors of 224:
1
2
4
8
14
16
28
32
56
112
224
With these values at our disposal as building blocks for calculations and problem-solving methods — both in academia and everyday life — we unlock endless possibilities.
For instance:
– Calculating percentages becomes simpler when using common factors.
– Simplifying fractions with large numerators or denominators becomes effortless.
– Solving word problems involving ratios or proportions becomes more manageable.
– Identifying common multiples or divisors helps streamline data analysis tasks.
– Working with measurements becomes more intuitive since many conversions rely on factoring numbers.
However useful they might be in practice though,
it’s important not to fall victim to challenges that arise when working with factors. One common mistake is overlooking certain factors or forgetting to consider negative numbers as well




